Denoising Diffusion Implicit Models
Abstract
DDIMs是一个更高效的迭代隐式概率模型,和DDPMs采用相同的训练过程
DDIMs通过一个非马尔可夫的扩散过程,从而实现相同的训练目标。这些非马尔可夫过程可以对应于确定性的生成过程,从而产生能更快地生成高质量样本的隐式模型
DDIMs相对DDPMs,生成样本的速度快了10x,甚至50x,可以生成高质量样本,最重要的是实现了inversion,图像重建误差非常小,可以在latent space进行插值实现图像的二次生成
Contributions
- 加速生成
- 隐空间重建与插值
Related Work
- DDPM
Methodology
Overview
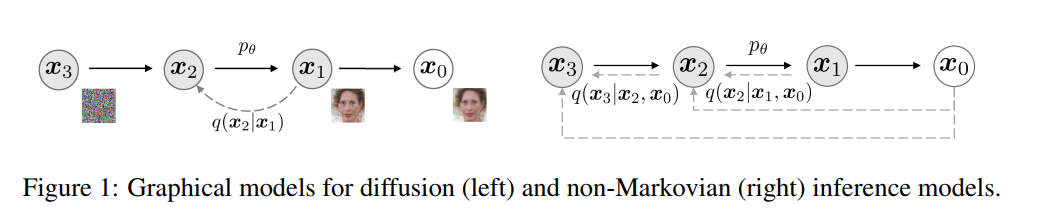
NON-MARKOVIAN FORWARD PROCESSES
- 扩散前向过程不再是马尔科夫过程(Xt只以来Xt-1),因为Xt依赖Xt-1和X0
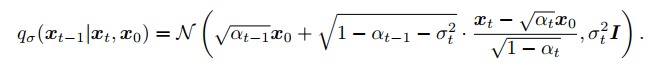
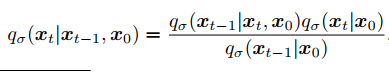
GENERATIVE PROCESS
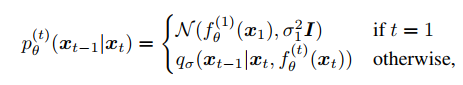
- a fixed prior pθ(xT ) = N(0; I)
UNIFIED VARIATIONAL INFERENCE OBJECTIVE
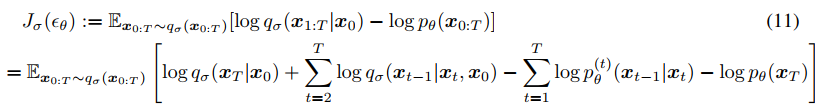
SAMPLING FROM GENERALIZED GENERATIVE PROCESSES
DENOISING DIFFUSION IMPLICIT MODELS
- one can generate a sample xt-1 from a sample xt
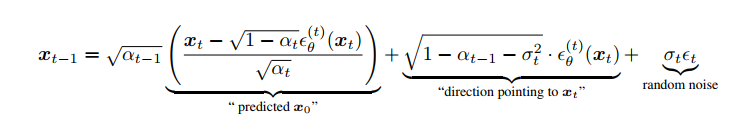
- 在所有 t 中 (t不等于1),σt = 0;给定 xt-1 和 x0,前向过程成为确定性过程。在生成过程中,随机噪声 t 前的系数变为零。由此产生的模型成为隐式概率模型,其中样本从潜在变量生成,其固定程序为(从 xT 到 x0)
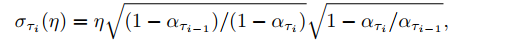
- 当 η = 1 时为 DDPM,当 η = 0 时为 DDIM
ACCELERATED GENERATION PROCESSES
- DDIM 优化时与 DDPM 一样,对噪声进行拟合,但 DDIM 提出了通过一个更短的 Forward Processes 过程,通过减少采样的步数,来加快采样速度
- 从原先的采样序列 {1,…,T} 中选择一个子序列来生成图像。如原序列为 1 到 1000,抽取子序列可以是 1, 100, 200, … 1000 (类似
arange(1, 1000, 100))。抽取方式不固定。在生成时同样采用公式 (1),其中的 timestep t ,替换为子序列中的 timestep。其中的 αˉt 对应到训练时候的数值,比如采样1, 100, 200, ... 1000中的第二个样本,则使用训练时候采用的 αˉ100 (此处只能替换alphas_cumprodˉαˉ,不能直接替换alpha参数 αt) - 参考论文中的 Figure 3,在加速生成的情况下,η 越小,生成的图片效果越好,同时 η 的减小能够很大程度上弥补采样步数减少带来的生成质量下降问题
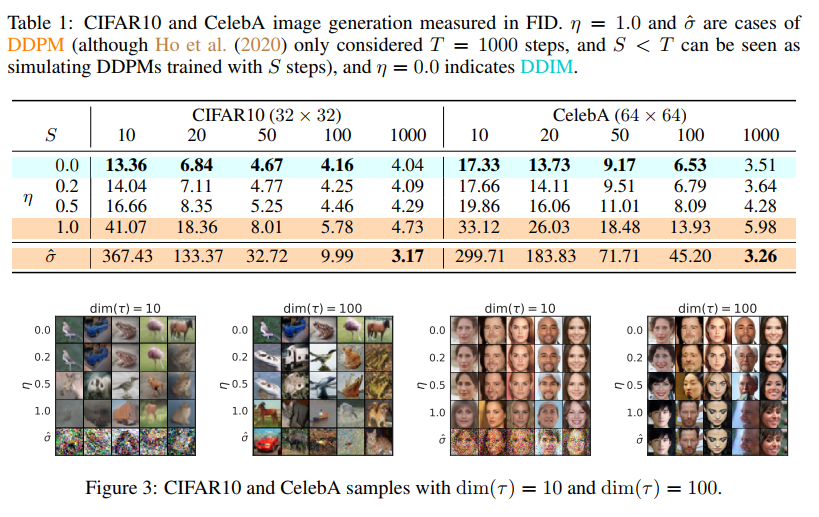
Experiments
- 重建和插值

Conclusions
DDIM是DDPM的泛化版本
DDIM不是马尔可夫链,把所有时间步方差=0,高斯噪声的随机性被移除了,变成了确定性采样
过于理论,应用场景
- 加速采样过程 (子序列采样,从T个时间步中采样一部分)
- 图像反演/重建 DDIM inversion (图像转换到隐空间,重建误差非常小)
- 图像插值 DDIM interpolations(不平滑)
References
- 实操 https://aistudio.baidu.com/projectdetail/5279888?channelType=0&channel=0
- 验证当 η=1 DDIM 提出的的采样方式结果与 DDPM 基本相同
- DDIM 的加速采样过程
- DDIM 采样的确定性及其插值



